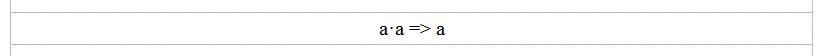A+B-AB Algebraic Boolean
A new way to calculate with Boolean.
Intro
This is a sort of Boolean Math I started developing a longer time ago
when I was active in the search for optimal Golomb ruler. I was in contact
with a group that searched those rulers by distributing the work on
multiple people and computers over the internet. This was before
distributed computing was common and it was before distributed.net picked
up this search. It was the time when the golomb ruler search program
GVANT was developed by Mark Garry and David Vanderschel and later
GARSP where I could do a significant contribution. GARSP = Garrys adaption
of Rado's search principle. Rado was my internet alias that I used
at that time and is deviated from the first letters of my first and last
name.
My original idea of this math was to use it to calculate optimal Golomb
rulers directly rather than haveing to find them through an intensive
brute force search. A Golomb ruler is a special set of natural numbers.
The basic idea was to express those natural numbers in binary form and
caclulate/generate the distances on a binary level directly using boolean
operations. Every distance can be represented through a boolean expression
containing the binary unknown of the base distances. If I can replace the
boolean values with real numbers and transform the Boolean operations into
a classic algebra arithmetic it should be possible to generate enough
equations to solve it for the binary unkown. This lead me to what I will
present you here.
I did one major mistake at that time and that was the idea that I have to
generate equations and solve the problem in the classic algebra space when
I go with my Boolean Math whereas in true if you stuck born finish the
path I took and transform the end back to the classic Boolean you end up
with the solution. I figured this out lately when I was looking on my
Boolean Math again for a problem in cryptography.
Equivalence
Everything I do with my new alternative Boolean Math (example solving for
an optimal Golomb ruler) can be done with classic Boolean algebra too.
There is no advantage in what is possible. It's just a different way to
deal with Boolean. My alternative Boolean Math is simpler to handle and
manage on a computer. Just think about how costy an inversion of a
Boolean expression with multiple terms is. In my alternative Boolean Math
it is just a 1 - (the expression).
However you do not spare space. If you have 8 Unknown you will have to
deal with up to 2^8 = 256 terms. And you will not spare calculation
time because a logic operation like AND or OR contains a multiplication
which means you have to multiply up to 256 * 256 terms in case of 8
unknown. Although those are not really multiplication you do like you will
see later.
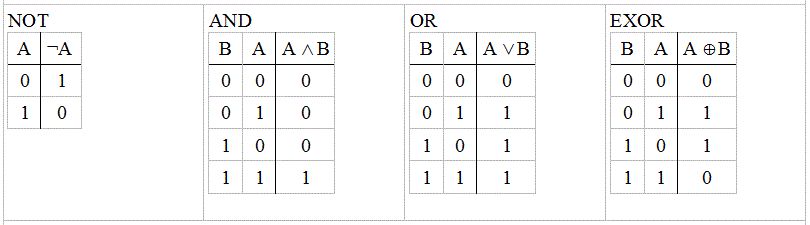
Classic Boolean
In classic Boolean we know this logic Operations:
where as in this Table the number 0 represents FALSE and the number 1
represents TRUE
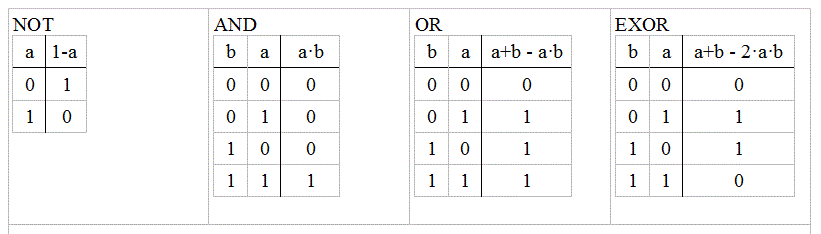
New Algebraic Boolean
I have no idea how to best call it.
We replace the Calssic Boolean Operation and Variable with algebraic
operations and variables. First we replace the Boolean values with real
number values like this:
The value transformation doesn't have to be like this. We could as
well transfer False into -1 and True into +1. However like we will see soon
the above is the only way our alternative Boolean Math will work.
With real numbers we can transfer our Boolean Operations into simple
algebra. Like you can easily verify the Truth Table stays correct with
this algebra expression
So we summarize the Boolean Operation to algebra terms:
We did not do any value restriction four our algebra variables yet. We are
allowed to do calculations with any real number. So insert
a=0.3, b=0.6 if you like and see what result you get.
But calculating the expressions with any other numbers than 0 and 1 which
represents our false and true in the Boolean Space is of no interest to us.
Now lets say we have this Boolean Expression: A ∧ ¬A
Like you know from classic Boolean Algebra this can be simplified to 0 or
FALSE.
How does it look in our Algebraic Boolean?
A => a
¬A => 1-a
A ∧ ¬A => a · (1- a) => a - a^2
Of course our result is correct because you can insert 0 for a and 1
for a and you will see you end up with 0 in both cases.
But that is certainly unsatisfying in every way.
First of we got a square and it is to expect that when we deal with more
unknown you will get all sort of terms with unlimited power.
Second the result did not simplify itself to 0.
One ugly thing with classic Boolean algebra is that you always have to do
clean up/reducing the Boolean expression after some operation (inverse for
example) and bringing them back into a simpler form where you can
continue calcuting.
This ugly Boolean behaviour was one of the reason I looked for
something else.
What is required is a Boolean Math that does self simplification.
After every calculation you automatical should end up cleared up result.
So we need to get right of any squares and powers.
Since we can have any power we should reduce every power to the same and
best simplest result which would be power of 1.
a^n => a
a^n shall be replaced with a. To be allowed to do that a^n has to be
equal a!
Now for any number in the set of real numbers it is not possible.
BUT we are lucky. There are 2 real number where a^n is equal a. And we only
need 2! It's the number 0 and the number 1.
So if we limit our variables (or focus of interest) in our algebra
terms to {0, 1} only, we may set a^n = a. (where n in our case is any
positive natural number without 0)
So we leave the pure algebra space and rules and add a RULE to our new
algebraic Boolean Math:
This is the most important addition and Rule and the core of this new
algebraic Boolean Math. Because this does all the magic:
A ∧ ¬A => a · (1- a) => a - a^2 =>
a - a => 0
We got rid of our power and we got the most
simple result and it will make sure (without prove) to my understanding
that we always get the one and only and simplest result.
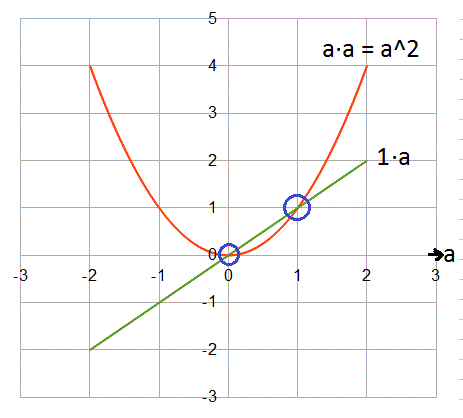
Our additional Rule did not change the outcome for any input number of 0
and 1. However it has of course changed the result for any other number
than 0 and 1. If you check about a - a^2 in the graphic above where I
have drawn a and a^2 you should be able to see it.
This is no advantage or disadvantage it's just something that doesn't
really bother us because all we are interested in are the two numbers 0
and 1. However the variables are not restricted to those and you still
may insert any real numbers. I explicit did not write a·a = a which is
only correct for 0 and 1 but made and arrow as replacing rule valid for
our focus of interest.
...so much for now.... we are not finish... there is more to come.
updated: 30.Jan.2013
created: 28.Jan.2013
email: radorni
@ solnet.ch